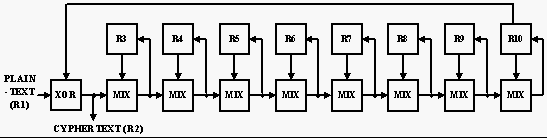
David Wheeler has agreed to this extension to WAKE's table generation. The cypher, decypher and hash functions are simple extensions to WAKE's original algorithms.

The generation of 8 Tables

The program below gives in C the routine that generates from the key k (length 8 words), the table t that is made up of 8 sub-tables. The length of t is 2049, although only 2048 words are used in coding and decoding.

The generation of the initial table t is similar to the original method, except that the table is 8 times larger. However, in the second phase, the table is divided into 8 for subsequent permutations.

genkey8(long t[], long k[])
{   int p, y;
    long x, z;
    static long tt[10]= { 0x726a8f3b, 0xe69a3b5c, 0xd3c71fe5, 0xab3c73d2,
                          0x4d3a8eb3, 0x0396d6e8, 0x3d4c2f7a, 0x9ee27cf3
                        };                             /* obfuscation table */

    for (p = 0; p < 8; p++)
        t[p] = k[p];                                /* copy key in to table */

    for (p = 8; p < 2048; p++)                                /* fill table */
    {   x = t[p - 8] + t[p - 1]; 
        t[p] = x >> 3 ^ tt[x & 7];               /* note effect if x is -ve */
    }

    for (p = 0; p < 23; p++)                           /* mix first entries */
        t[p] += t[p + 89];

    for (y = 0; y < 8; y++)                  /* process one table at a time */
    {   x = t[33 + y];
        z = t[59 + y] | 0x01000001;         /* top 8 bits are an odd number */
        z = z & 0xff7fffff;             /* bottom 23 bits are an odd number */

        for (p = y * 256; p < (y + 1) * 256; p++)
        {   x = (x & 0xff7fffff) + z;                    /* change top byte */
            t[p] = t[p] & 0x00ffffff ^ x;           /* to a permutation etc */
        }

        t[256 * (y + 1)] = t[256 * y];
        x &= 255;

        for (p = y * 256; p < (y + 1) * 256; p++)
        {   x = (t[p ^ x] ^ x) & 255;         /* further change permutation */
            t[p] = t[256 * y + x];                      /* and other digits */
            t[256 * y + x] = t[p + 1];
        }
    }
}

Encryption

The only difference between this algorithm and the original is that the number of stages has doubled.

cypher8(long V[], long n, long k[], long r[], long t[])
{   long r1, r2, r3, r4, r5, r6, r7, r8, r9, r10,              /* registers */
         d,                                                    /* direction */
         *e,
         mask = 0x00ffffff;

    r3 = k[0]; r4 = k[1]; r5 = k[2]; r6  = k[3];
    r7 = k[4]; r8 = k[5]; r9 = k[6]; r10 = k[7];

    if (n < 0) d = -1;
    else       d =  1;

    e = V + n;                                               /* end pointer */

    while (V - e)
    {   r1 = *V;
        r2 = r1 ^ r6;
        *V = r2;
        V += d;

        r3 = r3 + r2;                   /* (Change r2 into r1 for decoding) */
        r3 = (r3 >> 8 & mask) ^ t[r3 & 255];

        r4 = r4 + r3;
        r4 = (r4 >> 8 & mask) ^ t[256 + (r4 & 255)];

        r5 = r5 + r4;
        r5 = (r5 >> 8 & mask) ^ t[512 + (r5 & 255)];

        r6 = r6 + r5;
        r6 = (r6 >> 8 & mask) ^ t[768 + (r6 & 255)];

        r7 = r7 + r6;
        r7 = (r7 >> 8 & mask) ^ t[1024 + (r7 & 255)];

        r8 = r8 + r7;
        r8 = (r8 >> 8 & mask) ^ t[1280 + (r8 & 255)];

        r9 = r9 + r8;
        r9 = (r9 >> 8 & mask) ^ t[1536 + (r9 & 255)];

        r10 = r10 + r9;
        r10 = (r10 >> 8 & mask) ^ t[1792 + (r10 & 255)];
    }
    r[0] = r3; r[1] = r4; r[2] = r5; r[3] = r6;
    r[4] = r7; r[5] = r8; r[6] = r9; r[7] = r10;
}

Decryption

decypher8(long V[], long n, long k[], long r[], long t[])
{   long r1, r2, r3, r4, r5, r6, r7, r8, r9, r10,              /* registers */
         d,                                                    /* direction */
         *e,
         mask = 0x00ffffff;

    r3 = k[0]; r4 = k[1]; r5 = k[2]; r6  = k[3];
    r7 = k[4]; r8 = k[5]; r9 = k[6]; r10 = k[7];

    if (n < 0) d = -1;
    else       d =  1;

    e = V + n;                                               /* end pointer */

    while (V - e)
    {   r1 = *V;
        r2 = r1 ^ r6;
        *V = r2; 
        V += d;

        r3 = r3 + r1;     r3 = (r3 >> 8 & mask) ^ t[r3 & 255];
        r4 = r4 + r3;     r4 = (r4 >> 8 & mask) ^ t[256 + (r4 & 255)];
        r5 = r5 + r4;     r5 = (r5 >> 8 & mask) ^ t[512 + (r5 & 255)];
        r6 = r6 + r5;     r6 = (r6 >> 8 & mask) ^ t[768 + (r6 & 255)];

        r7 = r7 + r6;     r7 = (r7 >> 8 & mask) ^ t[1024 + (r7 & 255)];
        r8 = r8 + r7;     r8 = (r8 >> 8 & mask) ^ t[1280 + (r8 & 255)];
        r9 = r9 + r8;     r9 = (r9 >> 8 & mask) ^ t[1536 + (r9 & 255)];
        r10 = r10 + r9;  r10 = (r10 >> 8 & mask) ^ t[1792 + (r10 & 255)];
    }
    r[0] = r3; r[1] = r4; r[2] = r5; r[3] = r6;
    r[4] = r7; r[5] = r8; r[6] = r9; r[7] = r10;
}

Lack of Boundary Problems

It's worth noting at this point that if the length of the plaintext does not fall on a word (32-bit) boundary then there are no problems. In both the encryption and decryption routines, the output is calculated before the registers are updated. This means that in the final word, the register update is irrelevant and padding bytes make no difference to either the encryption or decryption processes.

Mode three cyphering is done by:

    cypher(V+n-1, -4, k1, r, t) ;
    cypher(V,      n, k1, r, t) ;
    cypher(V+n-1, -n, k2, r, t) ;

The cypher routine can encypher disjoint segments as if they were contiguous, by using a generated end key as the next start key. Thus for example we can put the head and tail for mode one wherever we please without moving the entire data structure.

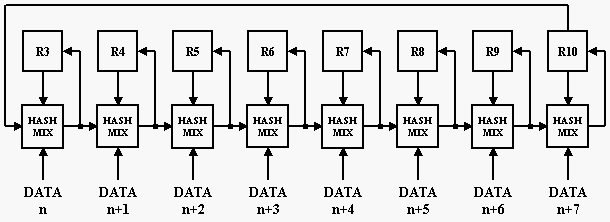
Use of the Keyed Hash

The routine hash8 uses the mix, table and key as for the cypher function. The end words are mixed at least three times, and there is overlap if the length is not a multiple of eight. This should make the hash nonlinearly dependant on all the data.

The following table shows what happens when the block length varies between multiples of eight.

hash8(long V[], long n, long k[], long r[], long t[])
{   long m, r3, r4, r5, r6, r7, r8, r9, r10,                   /* registers */
    *e,
    mask = 0x00ffffff;

    r3 = k[0]; r4 = k[1]; r5 = k[2]; r6  = k[3];
    r7 = k[4]; r8 = k[5]; r9 = k[6]; r10 = k[7];

    e = V + n - 7;                                           /* end pointer */

    for (m = 0; m < 4; m++)
    {   while (V < e)                        /* hash main part whilst m = 0 */
        {   r3 = (r3 ^ r6) + *V++;
            r3 = (r3 >> 8 & mask) ^ t[r3 & 255];

            r4 = (r4 ^ r3) + *V++;
            r4 = (r4 >> 8 & mask) ^ t[256 + (r4 & 255)];

            r5 = (r5 ^ r4) + *V++;
            r5 = (r5 >> 8 & mask) ^ t[512 + (r5 & 255)];

            r6 = (r6 ^ r5) + *V++;
            r6 = (r6 >> 8 & mask) ^ t[768 + (r6 & 255)];

            r7 = (r7 ^ r6) + *V++;
            r7 = (r7 >> 8 & mask) ^ t[1024 + (r7 & 255)];

            r8 = (r8 ^ r7) + *V++;
            r8 = (r8 >> 8 & mask) ^ t[1280 + (r8 & 255)];

            r9 = (r9 ^ r8) + *V++;
            r9 = (r9 >> 8 & mask) ^ t[1536 + (r9 & 255)];

            r10 = (r10 ^ r9) + *V++;
            r10 = (r10 >> 8 & mask) ^ t[1792 + (r10 & 255)];
        }
        V = e - 1;
    }
    r[0] = r3; r[1] = r4; r[2] = r5; r[3] = r6;
    r[4] = r7; r[5] = r8; r[6] = r9; r[7] = r10;
}

Plaintext Avalanche mode, using an initial block of 16 words:

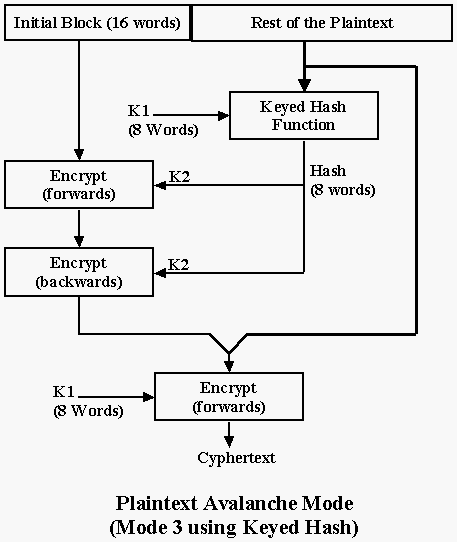
hash8 (V + 16, n - 16, k, r, t);               /* hash in r from n-16 words */
cypher8(V, 16, r, rr, t);                    /* rr is a dump of eight words */
cypher8(V + 15, -16, r, rr, t);         /* to fully mix first sixteen words */
                                 /* do basic cypher backwards then forwards */
cypher8(V, n, k, r, t);                         /* cypher the whole message */

with decode:

decypher8(V, n, k, r, t);
hash8(V + 16, n - 16, k, r, t);
decypher8(V + 15, -16, r, rr, t);
decypher8(V, 16, r, rr, t);

Note we do not now need to do the end block of words backwards, because the hash has a dependency on that block.

Also note that the sequence of events precludes the use of mechanisms that slowly change the tables. Incremental table modification can only happen when there is the single use of the encryption function.

In the paper, it's suggested that the whole table is recalculated every 10,000 words. This approximates to one change every 39 words. If 8 tables are used, then 8 mutually prime numbers around 39 can be used for determining the lengths of the incremental cycles.

Comments welcome:  Keith

Back to home page _{block,cipher,block cipher,crypto,cryptography,cipher design, encryption,word auto key,word autokey,WAKE,Hereward,David Wheeler, czczcz,DJ Wheeler,David J Wheeler}