The Message Authenticator Algorithm is, as far as the author
is aware, the first Cryptographic Hash Function or Message Digest
to gain widespread acceptance. It has become a part of ISO
standard 8731-2: Approved Algorithms for Message
Authentication. The designers were Donald Davies and David
Clayden.
A .pdf version is available.
This is a historical document - this algorithm should not
be used in modern systems. See appended notes for extra
material.
NPL Report DITC 109/88
February 1988

NATIONAL PHYSICAL LABORATORY
The Message Authenticator
Algorithm (MAA)
and its Implementation
by
D.W. Davies
Consultant, British Technology Group
and
D.O. Clayden
Consultant, British Technology Group
© Crown copyright 1988
ISSN 0262-5369
National Physical Laboratory
Teddington, Middlesex TW11 0LW, UK
Extracts from this report may be reproduced
provided the source is acknowledged
Approved on behalf of Director, NPL, by Dr T.G. Blaney
Superintendent, Division of Information Technology and Computing
CONTENTS
1 Introduction 1
2 Purpose of the Algorithm 2
3 Implementation Considerations 2
4 General Description 4
5 Specification of the Functions Used in the Algorithm 5
6 Definition of MUL1(X,Y) 6
7 Definition of MUL2(X,Y) 6
8 Definition of MUL2A(X,Y) 7
9 The Functions BYT{X,Y} and PAT{X,Y} 8
10 The Prelude 9
11 The Main Loop 10
12 The Coda 11
13 Mode of operation 11
14 Details of the Multiplication Functions 11
15 Test Examples For Parts of the Algorithm 12
16 Test Examples for MUL1, MUL2, MUL2A 13
17 Test Examples for BYT{X,Y} and PAT{X,Y} 14
18 Test Examples for the Prelude 15
19 Test Examples for the Main Loop 16
20 Test Examples for the Whole Algorithm 18
21 Diagram Showing Data Flow 20
22 Implementation in 'C' 21
23 Implementation in Basic 29
24 References 36
- 1 -
The Message Authenticator Algorithm (MAA) and its Implementation
by D.W. Davies and D.O. Clayden
1 Introduction
A message authenticator algorithm (MAA) was developed by D.W. Davies and
D.O. Clayden and published in 1983 [1]. The text of the original report
is reproduced below, updated a little to reflect events since its first
publication. Examples of programs for MAA are included in this
report. The algorithm attracted the attention of the Committee of the
London Clearing Banks and then Technical Committee 68 (Banking) of the
International Standards Organisation, which adopted it as one of the approved
algorithms for message authentication [2]. In the course of examining
the algorithm a number of bodies tested its level of security. One
potential attack was found, using a very large amount of chosen plain text in
very long and artificial messages. It is questionable whether such an
attack is realistic, since the ability of an adversary to subject an
algorithm, with its secret key, to almost unlimited testing with chosen text
would be a fatal weakness of an authenticated message scheme. Access to
such a facility must be strictly controlled.
To avoid even this attack, the ISO standard 8731-2 contains a limitation of
the total block of data to 1024 bytes and a 'mode of operation' in section 5
of the standard which chains these blocks together.
A long financial message can often be divided conveniently into segments
which are no longer than 1024 bytes - for example into a series of separate
payment messages. It is often preferable to provide each segment with
its own authenticator, in the same way that error control is often segmented
rather than covering a whole file. To detect insertion and deletion of
segments, consecutive sequence numbering and checking can be used.
Control totals, if authenticated, can prevent truncation at the end of the
file. Another method is to send a group authenticator calculated from
the sequence of segment authenticators. Groups of 256 segments can be
authenticated in this way and if necessary a hierarchy of such authentication
is possible, not limited to 1,000,000 blocks. This does not conflict
with ISO 8731-2 and is, in effect, an alternative mode of operation.
- 2 -
In the reproduction of the 1983 report given below, the ISO 'mode of
operation' has been inserted, and Table 4 is given in two versions 4(a)
decimal and 4(b) hexadecimal, to help those testing main loop
implementations. Table 5 of the original report contained an error in
the first two columns of row S. Details appear in a note below the
table. Unfortunately this error also occurs in the ISO version.
2 Purpose of the Algorithm
An 'authenticator' is a number which is sent with a message so that a check
can be made by the receiver of the message that it has not been altered since
it left the sender. For authenticators in general the sender and
receiver share the knowledge of a key K which is otherwise secret. If M
is the message, the authenticator is a function of K and M. It is
calculated by the sender and again by the receiver. If the receiver's
calculated value equals the authenticator value received with the message, the
message is assumed to be correct. When a well designed authenticator is
used, giving a 32 bit result, the probability that a message alteration will
not be detected is 2-32, which is small enough for most
purposes.
3 Implementation Considerations
The algorithm was originally designed to be implemented on a main frame
computer. In practice, implementations in high level languages have
often proved slow in operation. The advent of low cost computers (PCs or
similar) with larger word sizes increases the options for effective
implementation of MAA.
There have been several requests for a version of the MAA, or a new
algorithm, which could be implemented on a personal computer. The
development of a new algorithm for this purpose would be likely to take a
considerable time because of the amount of testing involved. Furthermore
the MAA can now be implemented on a PC at a useful speed.
Many users prefer a version written in a high level language. For the
highest speed the MAA needs to be written in assembly code, but the version in
this report written in 'C' has achieved speeds of about one millisecond per
message block of 32 bits on IBM compatible PCs of various types. This
report also includes a version written in Basic, primarily as a description of
the algorithm, and also to check results. It can be run on a BBC micro
or on an IBM compatible PC using the MTEC BBCBasic(86) interpreter which uses
32 bit values for all arithmetic and bitwise boolean functions.
- 3 -
The MAA has several special requirements which influence the choice of
language in which to write a program. In particular it needs:
Multiplication of two 32 bit unsigned numbers to produce a 64 bit
unsigned product.
Addition of two unsigned 32 bit numbers to produce a 32 bit sum and a
carry bit.
Boolean functions of 32 bit values.
Splitting 32 bit unsigned values into 8 bit bytes and concatenating
back to 32 bit values.
The language 'C' copes with all of these requirements except (1) and the
carry bit of (2). However it is capable of producing a 32 bit unsigned
product from the multiplication of two 16 bit values, and the carry bit from
addition can be derived from the most significant bits of the three values
involved.
Pascal has the disadvantage that the 32nd bit is treated as a sign bit and
a carry into the 33rd bit is reported as an overflow. Dealing with this
can add a considerable time penalty. (A similar situation usually exists
in Basic). We have not written an implementation in Pascal, but methods
of dealing with these problems are illustrated in the Basic program. In
particular, the function ADDU (unsigned addition) and the procedures MUL32 and
MUL16 could be used as models for a Pascal version. Early Pascal
compilers did not implement bitwise boolean functions, but these are now
available in Prospero Pascal version 3.
A version of the MAA has been written by D.W. Davies in assembly code for
the 6502. This takes about 6 milliseconds per message block using the
BBC model B. A version written by D.O. Clayden in Turbo Basic
(compiling) takes about 300 millisec per message block, about the same time as
the Basic program herein when run with the MTEC BBCBasic(86)
interpreter. The Turbo Basic program illustrates methods which are
applicable in dialects which lack 32 bit boolean functions. This version
and the 6502 version can be made available on request.
- 4 -
4 General Description
All numbers manipulated in this algorithm are regarded as 32 bit unsigned
integers, unless otherwise stated. For such a number N, 0 < N
< 232. This algorithm can be implemented conveniently and
efficiently in a computer with word length 32 bits or more.
The message can be a bit string of any length but for input to the
algorithm we regard it as a sequence of 32 bit numbers
M1, M2---Mn of which there are n, called
'message blocks'. The detail of how to pad out the last block
Mn to 32 bits is not part of the algorithm but must be defined in
any application. No weakness is introduced by choosing one of the
simplest rules, such as extending to the right or left with zeros or ones.
During the process of testing and evaluation of this algorithm, it was
found that its use for very long messages results in some reduction of the
dependence of the authenticator on the early data in the message. To
minimise this effect, ISO 8731-2 specifies that the algorithm shall not be
used for messages with more than 1,000,000 blocks, i.e. n should not exceed
1,000,000. Note the 'mode of operation' which is applied to messages
longer than 1024 bytes (n>256).
The key consists of two 32 bit numbers J and K and thus has a size of 64
bits.
The result of the algorithm is a 32 bit authenticator value denoted
Z. The calculation can be performed on messages as short as one block
(n=1).
The calculation, a flow diagram of which is shown on page 20, has three
parts:
- 5 -
- The 'Prelude' is a calculation made
with the keys (J and K) alone and it generates six numbers X0,
Y0, V0, W, S and T which are used in the subsequent
calculations. This part need not be repeated until a new key is
installed.
- The 'Main loop' is a calculation which is repeated for each message
block Mi, therefore for long messages it dominates the
calculation.
- The 'Coda' consists of two operations of the main loop using as its
'message blocks' the two numbers S and T in turn, followed by a simple
calculation of Z, the authenticator.
Therefore the processing load of the algorithm contains a part (the main
loop and coda) proportional to n+2 where n is the message size, and a constant
overhead each time the keys are changed.
5 Specification of the Functions Used in the Algorithm
A number of functions are used in the description of the algorithm.
In the following, X and Y are 32 bit numbers and the result is a 32 bit number
except where stated otherwise.
CYC(X) is the result of a one-bit cyclic left shift of X.
AND(X,Y) is the result of the logical AND operation carried out on
each of 32 bits.
OR(X,Y) is the result of the logical OR operation carried out on
each of 32 bits.
XOR(X,Y) is the result of the XOR operation (modulo 2 addition)
carried out on each of 32 bits.
ADD(X,Y) is the result of adding X and Y discarding any carry from
the 32nd bit, that is to say, addition modulo 232.
CAR(X,Y) is the value of the carry from the 32nd bit when X is
added to Y, it has the value 0 or 1.
MUL1(X,Y), MUL2(X,Y) and MUL2A(X,Y) are three different
forms of multiplication, each with a 32 bit result.
To explain these multiplications, let the 64 bit product of X and Y be
{U,L}. Here the curly brackets mean that the values enclosed are
'concatenated', U on left of L. Hence U is the upper (most significant)
half of the product and L the lower half.
- 6 -
6 Definition of MUL1(X,Y)
Multiply X and Y to produce {U,L}. With S and C as local
variables,
S:=
ADD(U,L); (1)
C:=
CAR(U,L); (2)
MUL1(X,Y):= ADD(S,C) (3)
That is to say, U is added to L with 'end around carry'.
Numerically the result is congruent to X*Y, the product of X and Y, modulo
(232-1). This can be seen by the following argument. It
is not necessarily the smallest residue because it may equal
232-1.
X*Y = 232U + L
S = U + L - 232C
from (1) and (2)
MUL1(X,Y) = S + C
= U + L -
(232 - 1)C
= X*Y - (232
- 1)(U + C)
It is shown later that the addition (3) cannot produce a carry from the
32nd bit (see 'details of the multiplication functions').
7 Definition of MUL2(X,Y)
This form of multiplication is not used in the main loop, only in the
prelude. With D, E, F, S and C as local variables,
D:=
ADD(U,U); (4)
E:=
CAR(U,U); (5)
F:=
ADD(D,2E); (6)
S:=
ADD(F,L); (7)
C:=
CAR(F,L); (8)
MUL2(X,Y):= ADD(S,2C) (9)
- 7 -
Numerically the result is congruent to X*Y, the product of X and Y, modulo
(231-2). This can be seen by the following argument. It
is not necessarily the smallest residue because it may equal
231-2.
X*Y = 232U + L
2U =
D + 232E from (4) and (5)
F = D + 2E from (6)
F + L = S + 232C
from (7) and (8)
MUL2(X,Y) = S + 2C from (9)
= F + L - (232 - 2)C
= D + 2E + L -
(232 - 2)C
= 2U + L -
(232 - 2)(E + C)
= X*Y -
(232 - 2)(U + E + C)
It is shown later that additions (6) and (9) cannot produce a carry from
the 32nd bit (see 'details of the multiplication functions').
8 Definition of MUL2A(X,Y)
This is a simplified form of MUL2(X,Y) used in the main loop, which yields
the correct result only when at least one of the numbers X and Y has a zero in
its most significant bit.
It is employed for economy in processing. D, S, C are local
variables.
D:= ADD(U,U); (10)
S:= ADD(D,L); (11)
C:= CAR(D,L); (12)
MUL2A(X,Y):= ADD(S,2C) (13)
The result is congruent to X*Y modulo (231-2) under the
conditions stated because, in the notation of MUL2(X,Y) above, the carry E =
0. This will be shown later (see 'details of the multiplication
functions').
- 8 -
9 The Functions BYT{X,Y} and PAT{X,Y}
A procedure is used in the 'prelude' to condition both the keys and the
results in order to prevent long strings of ones or zeros. It produces
two results which are the conditioned values of X and Y and a number PAT{X,Y}
which records the changes that have been made. PAT{X,Y} < 255
so it is essentially an 8 bit number.
X and Y are regarded as strings of bytes. Using the notation {X,Y...}
for concatenating,
{X,Y} =
{B0,B1,B2,B3,B4,B5,B6,B7}
Thus bytes B0 - B3 are derived from X and
B4 - B7 from Y.
The procedure is best described by a program where each byte Bi
is regarded as an integer of length 8 bits:
P:= 0;
for i:= 0 to 7 do
begin
P:= 2 * P;
if Bi = 0 then
begin
P:= P + 1;
B'i:= P
end
else if Bi = 255 then
begin
P:= P + 1;
B'i = 255 - P
end
else
B'i:= Bi
end;
The results are:
BYT{X,Y} =
{B'0,B'1,B'2,B'3,B'4,B'5,B'6,B'7}
and PAT{X,Y} = P
Examples for checking an implementation of this function are given
later.
- 9 -
10 The Prelude
{J1,K1} := BYT{J,K};
P := PAT{J,K}; (14)
Q := (1+P)*(1+P)
First, a calculation using J1 produces H4,
H6 and H8 from which X0, V0 and S
are derived.
J12:= MUL1(J1,J1); J22:= MUL2(J1,J1);
J14:= MUL1(J12,J12); J24:= MUL2(J22,J22);
J16:= MUL1(J12,J14); J26:= MUL2(J22,J24); (15)
J18:= MUL1(J12,J16); J28:= MUL2(J22,J26);
H4:= XOR(J14,J24);
H6:= XOR(J16,J26); (16)
H8:= XOR(J18,J28);
A similar calculation using K1 produces H5,
H7 and H9, from which Y0, W and T are
derived.
K12:= MUL1(K1,K1); K22:= MUL2(K1,K1);
K14:= MUL1(K12,K12); K24:= MUL2(K22,K22);
K15:= MUL1(K1,K14); K25:= MUL2(K1,K24); (17)
K17:= MUL1(K12,K15); K27:= MUL2(K22,K25);
K19:= MUL1(K12,K17); K29:= MUL2(K22,K27);
H0:= XOR(K15,K25);
H5:= MUL2(H0,Q);
H7:= XOR(K17,K27); (19)
H9:= XOR(K19,K29);
Finally, the results are conditioned by the BYT function:
{X0,Y0} := BYT{H4,H5};
{V0,W} := BYT{H6,H7}; (20)
{S,T} := BYT{H8,H9}
Examples are given later for checking this part of the algorithm, except
for lines (14).
- 10 -
11 The Main Loop
This loop is performed in turn for each of the message blocks
Mi. In addition to Mi, the principal values
employed are X and Y and the main results are the new values of X and Y.
It also uses V and W and modifies V at each performance. Note that X, Y
and V are initialised with the values provided by the Prelude. In order
to use the same keys again, the initial values of X, Y and V must be
preserved, therefore they are denoted X0, Y0 and
V0 and there is an initialising step X:= X0, Y:=
Y0, V:= V0, after which the main loop is entered for the
first time. The 'coda', used after all message blocks have been
processed by n cycles of the loop, is described in the next section.
The program is shown in columns to clarify its 'parallel' operation but it
should be read in normal reading order, left to right on each line
V:= CYC(V); (21)
E:= XOR(V,W); (21)
X:= XOR(X,Mi); Y:= XOR(Y,Mi); (22)
F:= ADD(E,Y); G:= ADD(E,X); (23)
F:= OR(F,A); G:= OR(G,B); (23)
F:= AND(F,C); G:= AND(G,D); (23)
X:= MUL1(X,F); Y:= MUL2A(Y,G) (24)
The numbers A, B, C, D are constants which are, in hexadecimal
notation:
Constant A: 0204 0801
Constant B: 0080 4021
Constant C: BFEF 7FDF
Constant D: 7DFE FBFF
Lines (21) are common to both paths. Line (22) introduces the message
block Mi. Lines (23) prepare the multipliers and line (24)
generates new X and Y values. Only X, Y and V are modified for use in
the next cycle. F and G are local variables. Since the constant D
has its most significant digit zero, G < 231 and this ensures
that MUL2A in line (24) will give the correct result, a multiplication modulo
231 - 1.
- 11 -
12 The Coda
After the last message block Mn has been processed, the main
loop is performed with 'message block' S, then again with block T, i.e.
Mn+1 = S, Mn+2 = T.
After this, the authenticator is calculated as Z = XOR(X,Y) and the
algorithm is complete. The values X0, Y0,
V0, W, S and T should be retained in order to calculate further
authenticator values without repeating the prelude (key calculation) until the
keys are changed.
13 Mode of operation
ISO 8731-2 contains this mode of operation for messages longer than 1024
bytes. The word 'segment' is used here to avoid confusion with the
blocks Bi of 4 bytes.
Messages longer than 1024 bytes shall be divided into segments of 1024
bytes and chained as follows:
For the first segment of 1024 bytes the MAC (4 bytes) shall be
formed. The MAC value shall be prefixed to (but not transmitted in) the
second segment and the resultant 1028 bytes authenticated. This
procedure shall continue, with the MAC of each segment prefixed to the next,
until the last segment, which need not be of size 1024 bytes, and the final
MAC shall be used as the transmitted MAC for the whole message.
14 Details of the Multiplication Functions
Recalling that X*Y produces the 64 bit product {U,L},
If X,Y < 232-1, X*Y
< 264-233 + 1
Hence U < 232-2
and L < 232-1, i.e. no restriction
1 In the calculation of MUL1(X,Y)
232C + S = U + L <
233-3 from (1) and (2)
If a carry occurs, C = 1 and S < 232-3
Hence MUL1(X,Y) = S + C <
232-2 can produce no carry
- 12 -
2 In the calculation of MUL2(X,Y)
232E + D = 2U <
233-4 from (4) and (5)
If a carry is produced, E = 1 and D <
232-4
Hence F = D + 2E < 232-2 can
produce no carry
If no carry is produced F = 2U is even and less
than 232
Hence F < 232-2 in either case
Also 232C + S = F + L <
233-3 from (7) and (8)
If a carry is produced, C = 1 and S <
232-3
Hence MUL2(X,Y) = S + 2C <
232-1 can produce no carry
3 In the calculation of MUL2A(X,Y) where X <
232-1, Y < 231-1
X*Y <
263-232-231 + 1
Hence U < 231-1,
2U < 232-2 can produce no carry
232C + S =
D + L = 2U + L < 233-3
If a carry is produced, C = 1 and S <
232-3
Hence MUL2A(X,Y) = S + 2C <
232-1 can produce no carry
15 Test Examples For Parts of the Algorithm
For most parts of the algorithm, simple test examples are given. The
data used are not always realistic, i.e. they are not values which could be
produced by earlier parts of the algorithm, and artificial values of constants
are used. This is done to keep the test cases so simple that they can be
verified by a pencil and paper calculation and thus the verification of the
algorithm's implementations does not consist of comparing one machine
implementation with another. The parts thus tested are:
MUL1, MUL2, MUL2A
BYT{X,Y} and PAT{X,Y}
Prelude, except the initial BYT{J,K} operation
Main loop
The Coda is not tested separately because it uses only the main loop and
one XOR function. For testing the whole algorithm, some results of test
runs with the NPL implementation are given, but it would be difficult to test
even the simplest case of the complete algorithm by pencil and paper
calculation.
- 13 -
16 Test Examples for MUL1, MUL2, MUL2A
It is suggested that the multiplication operations should be tested with
very small numbers and very large numbers. To represent a large number
we use the ones complement. Thus if a is a small number (say less than
4096) we use the notation ~a to mean its ones complement, i.e.
232 - 1 - a. Examples for testing MUL1, MUL2 and MUL2A are
given in Table 1.
For small numbers a and b, all three multiplication functions produce their
true product a*b. When large numbers are used the functions can give
different results. They should be tested both ways round, with MUL(x,y)
and MUL(y,x) to verify that these are equal.
(1) Test cases for MUL1
In modulo 232 - 1 arithmetic ~a is effectively -a, therefore the
results are very simple
MUL1(~a,b) = MUL1(a,~b) = ~(a*b)
MUL1(~a,~b) = a*b
(2) Test cases for MUL2
MUL2(~a,b) = ~(a*b - b + 1)
MUL2(a,~b) = ~(a*b - a + 1)
MUL2(~a,~b) = a*b - a - b + 1
(3) Test cases for MUL2A
This will give the same result as MUL2 when tested with numbers within its
range. For testing with large numbers,
~a and ~b - 231 must be used.
MUL2A(~a,b) = ~(a*b - b + 1)
MUL2A(a,~b) = ~(a*b - a + 1)
MUL2A(~a,~b-231) = 231(1 - p) + a*b + p - b - 1
where p is the parity of a; the value of its least significant bit.
That is, for even values of a the result is 231 + a*b - b - 1
for odd values of a the result is a*b - b
- 14 -
|
a |
b |
result |
MUL1
|
0000 000F
FFFF FFF0
FFFF FFF0 |
0000 000E
0000 000E
FFFF FFF1 |
0000 00D2
FFFF FF2D
0000 00D2 |
MUL2
|
0000 000F
FFFF FFF0
FFFF FFF0 |
0000 000E
0000 000E
FFFF FFF1 |
0000 00D2
FFFF FF3A
0000 00B6 |
MUL2A
|
0000 000F
FFFF FFF0
7FFF FFF0
FFFF FFF0 |
0000 000E
0000 000E
FFFF FFF1
7FFF FFF1 |
0000 00D2
FFFF FF3A
8000 00C2
0000 00C4 |
Table 1 Test cases for Multiplication Functions (hexadecimal)
17 Test Examples for BYT{X,Y} and PAT{X,Y}
Three cases for testing these functions are listed in Table 2
|
X |
Y |
{X,Y}
BYT{X,Y}
PAT{X,Y} |
00 00 00 00
01 03 07 0F
FF |
00 00 00 00
1F 3F 7F FF
|
{X,Y}
BYT{X,Y}
PAT{X,Y} |
FF FF 00 FF
FE FC 07 F0
FF |
FF FF FF FF
E0 C0 80 00
|
{X,Y}
BYT{X,Y}
PAT{X,Y} |
AB 00 FF CD
AB 01 FC CD
6A |
FF EF 00 01
F2 EF 35 01
|
Table 2 Test cases for the BYT and PAT Functions
- 15 -
18 Test Examples for the Prelude
An example is given in Table 3. The initial BYT{J,K} operation is not
tested. We assume that the results from lines (14) are
J1 = 0000 0100, K1 = 0000 0080, P = 1,
J12 0001 0000 J22 0001 0000
J14 0000 0001 J24 0000 0002
J16 0001 0000 J26 0002 0000
J18 0000 0001 J28 0000 0004
H4 0000 0003
H6 0003 0000
H8 0000 0005
K12 0000 4000 K22 0000 4000
K14 1000 0000 K24 1000 0000
K15 0000 0008 K25 0000 0010
K17 0002 0000 K27 0004 0000
K19 8000 0000 K29 0000 0002
H0 0000 0018
H5 0000 0060 (Q = 4)
H7 0006 0000
H9 8000 0002
{X0,Y0} 0103 0703 1D3B 7760 PAT{X0,Y0} EE
{V0,W} 0103 050B 1706 5DBB PAT{V0,W} BB
{S,T} 0103 0705 8039 7302 PAT{S,T} E6
Table 3 Test cases for lines (15) - (20) of the Prelude
The PAT values obtained from conditioning the results of the prelude are
quoted above for checking purposes but are not used in the algorithm.
- 16 -
19 Test Examples for the Main Loop
In Table 4, three examples of single block messages are given, using small
and large numbers. There are two versions of Table 4, 4a in decimal and
4b in hexadecimal notation. In the decimal table there is a convention
that ~a is 232 - 1 - a. In the third example there are two
cases of large numbers which must have zero in the 32nd bit, shown as ~2 -
231 and ~3 - 231 respectively. They could have
been written 231 - 2 and 231 - 3 respectively. In
order to keep the numbers small, artificial values of the constants A, B, C
and D are used. Three single block examples are followed by a message of
three blocks, in order to check that the implementation correctly retains the
value of X, Y and W. The final S and T cycles of the coda are not
included in this table.
Single block messages
Three-block message
A B
C D
V W
X0 Y0
M |
4 1
~8 ~4
3 3
2 3
5 |
1 4
~6 ~3
3 3
~2 ~3
1 |
1 2
~1 ~2*
7 7
~2 ~3
8 |
2 1
~4 ~4
1 1
1 2
0 |
2 1
~4 ~4
2 1
3 2
1 |
2 1
~4 ~4
4 1
20 9
2 |
|
V
E
X Y
F G
F G
F G
X Y
Z |
6
5
7 6
11 12
15 13
7 9
49 54
7 |
6
5
~3 ~2
2 1
3 5
1 4
~3 ~5
6 |
14
9
~10 ~11
~2 ~1
~2 ~1
~3 ~3*
30 30
0 |
2
3
1 2
5 4
7 5
3 1
3 2
1 |
4
5
2 3
8 7
10 7
10 3
20 9
29 |
8
9
22 11
20 31
22 31
18 27
396 297
165 |
CYC
XOR
XOR
ADD
OR
AND
MUL
XOR |
* - 231
Table 4a Test Cases for the Main Loop (decimal)
- 17 -
Single block
messages
Three-block message
A
B
C
D
V
W
X0
Y0
M |
4 1
1
1 4
2
FFFFFFF7 FFFFFFF9 FFFFFFFE
FFFFFFFB FFFFFFFC 7FFFFFFD
3 3
7
3 3
7
2 FFFFFFFD FFFFFFFD
3 FFFFFFFC FFFFFFFC
5 1
8 |
2 2
2
1 1
1
FFFFFFFB FFFFFFFB FFFFFFFB
FFFFFFFB FFFFFFFB FFFFFFFB
1 2
4
1 1
1
1 3
14
2 2
9
0 1
2 |
V
E
X
Y
F
G
F
G
F
G
X
Y
Z |
6 6
E
5 5
9
7 FFFFFFFC FFFFFFF5
6 FFFFFFFD FFFFFFF4
B 2 FFFFFFFD
C 1 FFFFFFFE
F 3 FFFFFFFD
D 5 FFFFFFFE
7 1 FFFFFFFC
9 4 7FFFFFFC
31 FFFFFFFC 1E
36 FFFFFFFA 1E
7 6
0 |
2 4
8
3 5
9
1 2
16
2 3
B
5 8
14
4 7
1F
7 A
16
5 7
1F
3 A
12
1 3
1B
3 14
18C
2 9
129
1 1D
A5 |
Table 4b Test Cases for the Main Loop (hexadecimal)
- 18 -
20 Test Examples for the Whole Algorithm
Using the NPL implementation of the algorithm, the four test examples with
two block messages given in Table 5 were calculated. For ease of
checking, intermediate results are tabulated: the results of the prelude and
the X and Y values after each operation of the main loop, that is for
M1, M2, S and T.
J
K
P
X0
Y0
V0
W
M1
X
Y
M2
X
Y
S
X
Y
T
X
Y
Z |
00FF 00FF
0000 0000
FF
4A64 5A01
50DE C930
5CCA 3239
FECC AA6E
5555 5555
48B2 04D6
5834 A585
AAAA AAAA
4F99 8E01
BE9F 0917
51ED E9C7
3449 25FC
DB91 02B0
24B6 6FB5
277B 4B25
D636 250D
F14D 6E28 |
00FF 00FF
0000 0000
FF
4A64 5A01
50DE C930
5CCA 3239
FECC AA6E
AAAA AAAA
6AEB ACF8
9DB1 5CF6
5555 5555
270E EDAF
B814 2629
51ED E9C7
2990 7CD8
BA92 DB12
24B6 6FB5
28EA D8B3
81D1 0CA3
A93B D410 |
5555 5555
5A35 D667
00
34AC F886
7397 C9AE
7201 F4DC
2829 040B
0000 0000
2FD7 6FFB
550D 91CE
FFFF FFFF
A70F C148
1D10 D8D3
9E2E 7B36
B1CC 1CC5
29C1 485F
1364 7149
288F C786
9115 A558
B99A 62DE |
5555 5555
5A35 D667
00
34AC F886
7397 C9AE
7201 F4DC
2829 040B
FFFF FFFF
8DC8 BBDE
FE4E 5BDD
0000 0000
CBC8 65BA
0297 AF6F
9E2E 7B36
3CF3 A7D2
160E E9B5
1364 7149
D048 2465
7050 EC5E
A018 C83B |
Table 5 Test Cases for the Whole Algorithm
Note. Table 5 of the original report contained an error in the
first two columns of row S. The values 51ED E967 (twice) should have
been 51ED E9C7.
- 19 -
A further set of test cases for the whole algorithm is given in Table
6. The J and K values were chosen to give long strings of zeros after
conditioning. The message consists of 20 blocks of zeros.
Intermediate values of X and Y are listed as well as the final authenticator
value Z.
J = 8001 8001, K = 8001 8000
block
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
S
T |
303F F4AA
55DD 063F
51AF 3C1D
A44A AAC0
4D53 901A
5F38 EEF1
F023 9DD5
EB35 B97F
4DA1 24A1
7F83 9576
11A9 D254
D880 4CA5
3F6F 7248
ACBC 13DD
4CE9 33E1
C1ED 90DD
3CD5 4DEB
BBA5 7835
D784 3FDC
5EBA 06C2
1D9C 9655
7BC1 80AB |
1277 A6D4
4C49 AAE0
5BC0 2502
63C7 0DBA
2E80 AC30
2A60 91AE
3DD8 1AC6
9372 CDC6
C6B1 317E
74B3 9176
D786 34BC
FDC1 A8BA
11AC 46B8
33D5 A466
C21A 1846
CD95 9B46
613F 8E2A
07C7 2EAA
6AD6 E8A4
9189 6CFA
98D1 CC75
A0B8 7B77 |
DB79 FBDC |
all message blocks are zeros
Table 6 Test case for a 20 block message
- 20 -
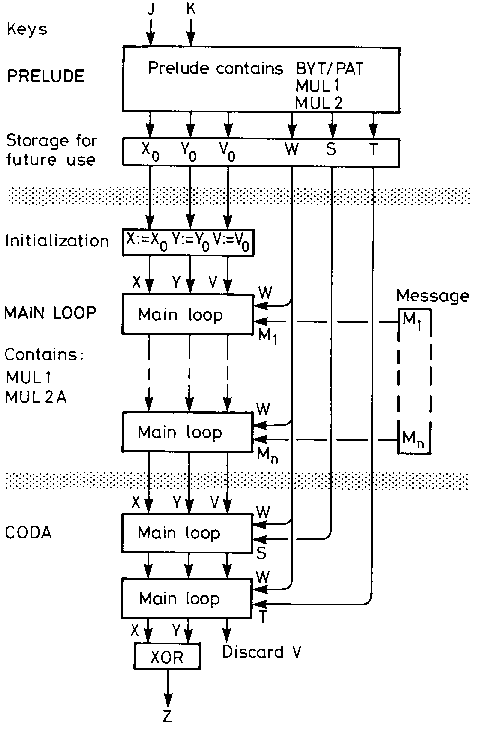
21 Diagram showing data flow
- 21 -
22 Implementation in 'C'
The 'C' program is written in the form of a series of functions or
procedures with a main program designed to run the tests described
above. The larger functions described in the algorithm are implemented
as functions or procedures, but the smaller ones, such as ADD, AND and CAR,
are implemented in a single line of code. Two versions of the mainloop
are provided called 'mainloop1' which outputs intermediate values for
checking, and 'mainloop2' which is designed for maximum speed. The
latter includes versions of mul1 and mul2a copied in full to avoid the time
taken to call the functions.
'C' does not provide the carry bit from the addition of two unsigned
values, but there are many ways of deriving it. The method used was
selected after speed trials.
The function mul32 employs shifts of 16 bits. An alternative method
is to employ a 'union' to access the halves of an unsigned long
variable. However with the Turbo and Zorland compilers this takes longer
than the method shown.
Those wishing to use the functions or procedures will need to write their
own main program to cope with input and output.
A time measurement option has been included although time measurement is
not part of standard 'C' and involves accessing the operating system.
Inaccuracies of about a tenth of a second are likely, so measurements of short
time intervals should be treated with reserve. The method 'guesstime'
has been chosen as it is likely to be portable. It uses the one second
clock in MS-DOS, and interpolates for fractions of a second.
The time measured for the main loop on IBM compatibles is approximately 1
millisec when compiled by the Turbo compiler and 1.1 millisec when compiled by
the Zorland compiler.
Time measurement may need alternative methods when using compilers other
than Turbo or Zorland, or operating systems other than MS-DOS.
- 22 -
/* MAA Message Authenticator Algorithm by D W Davies, NPL 1983. */
/* Version in C by D O Clayden, NPL 1987. */
/* Copyright NPL 1987 */
/* Version MAA7C22 suitable for running all tests and timing. */
/* Most printf statements are for test purposes only. */
/* Mainloop time about 1 millisec excl input, on M24 and PC1512. */
#include <stdio.h>
#include <time.h>
#include <dos.h>
#define BIT31 0x80000000L
#define FFFF 0xFFFFL
unsigned long a,b,c,d,l,m,s,t,u,v,w,x,y,z,pat,sum,t4,t5,v0,x0,y0;
int menu1()
{
int m;
printf(" 1 Test small functions (Tables 1,2)\n");
printf(" 2 Test prelude (Table 3)\n");
printf(" 3 Test main (Table 4)\n");
printf(" 4 Test prelude + main + coda (Table 5)\n");
printf(" 5 Test and timing of repeated message blocks (Table 6)\n");
printf(" 6 Quit to C \n");
scanf("%d",&m);
return(m);
} /* menu1 */
void mul32(a,b)
unsigned long a,b;
/* unsigned 64 bit product in u(upper) and l(lower) */
{
unsigned long p1,p2,p3,sum;
p1=(a&FFFF)*(b&FFFF);
p2=(a&FFFF)*(b>>16);
p3=(a>>16)*(b&FFFF);
sum=(p1>>16)+(p2&FFFF)+(p3&FFFF);
l=(p1&FFFF)+(sum<<16);
u=(sum>>16)+(p2>>16)+(p3>>16)+((a>>16)*(b>>16));
} /* mul32 */
- 23 -
unsigned long mul1(a,b)
unsigned long a,b;
{
unsigned long s,car;
mul32(a,b);
s=u+l;
car=((u^l)&BIT31)? !(s&BIT31):(u&BIT31)!=0;
return(s+car);
} /* mul1 */
unsigned long mul2(a,b)
unsigned long a,b;
{
unsigned long d,f,s,car;
mul32(a,b);
d=u+u; car=(u&BIT31)!=0;
f=d+car+car;
s=f+l;
car=((f^l)&BIT31)? !(s&BIT31):(f&BIT31)!=0;
return(s+car+car);
} /* mul2 */
unsigned long mul2a(a,b)
unsigned long a,b;
{
unsigned long d,s,car;
mul32(a,b);
d=u+u;
s=d+l;
car=((d^l)&BIT31)? !(s&BIT31):(d&BIT31)!=0;
return(s+car+car);
} /* mul2a */
void byt(x,y)
unsigned long x,y;
{
unsigned long p;
int i,b[8];
for (i=3; i>=0; i--) {
b[i]=x&255; b[i+4]=y&255;
x=x>>8; y=y>>8;
}
p=0;
for (i=0; i<8; i++) {
p=p+p;
if (b[i]==O) {p+=1; b[i]=p;} else if (b[i]==255) {p+=1; b[i]=255-p;}
}
pat=p; x=0; y=0;
for (i=0; i<4; i++) {
x=(x<<8)+b[i]; y=(y<<8)+b[i+4];
}
u=x; l=y;
} /* byt */
- 24 -
void prelude(x,y,test)
unsigned long x,y;
int test;
{
unsigned long j1[10],j2[10],k1[10],k2[10],h[10];
unsigned long p,q;
byt(x,y);
j1[0]=u; k1[0]=l; p=pat;
if (test>0) {
j1[0]=x; k1[0]=y;
printf("Enter P (2 hex): \n");
scanf("%X",&p);
}
q=(p+1)*(p+1);
j1[2]=mul1(j1[0],j1[0]); j2[2]=mul2(j1[0],j1[0]);
j1[4]=mul1(j1[2],j1[2]); j2[4]=mul2(j2[2],j2[2]);
j1[6]=mul1(j1[2],j1[4]); j2[6]=mul2(j2[2],j2[4]);
j1[8]=mul1(j1[2],j1[6]); j2[8]=mul2(j2[2],j2[6]);
h[4]=j1[4]^j2[4]; h[6]=j1[6]^j2[6]; h[8]=j1[8]^j2[8];
printf("H4= %lX \n",h[4]);
printf("H6= %lX \n",h[6]);
printf("H8= %lX \n",h[8]);
k1[2]=mul1(k1[0],k1[0]); k2[2]=mul2(k1[0],k1[0]);
k1[4]=mul1(k1[2],k1[2]); k2[4]=mul2(k2[2],k2[2]);
k1[5]=mul1(k1[0],k1[4]); k2[5]=mul2(k1[0],k2[4]);
k1[7]=mul1(k1[2],k1[5]); k2[7]=mul2(k2[2],k2[5]);
k1[9]=mul1(k1[2],k1[7]); k2[9]=mul2(k2[2],k2[7]);
h[0]=k1[5]^k2[5]; h[5]=mul2(h[0],q); h[7]=k1[7]^k2[7]: h[9]=k1[9]^k2[9];
printf("H0= %lX \n",h[0]);
printf("H5= %lX \n",h[5]);
printf("H7= %lX \n",h[7]);
printf("H9= %lX \n",h[9]);
byt(h[4],h[5]);
x0=u; y0=l;
printf("X0= %lX",x0);
printf(" Y0= %lX",y0);
printf(" PAT= %lX \n",pat);
byt(h[6],h[7]);
v0=u; w=l;
printf("V0= %lX",v0);
printf(" W= %lX",w);
printf(" PAT= %lX \n",pat);
byt(h[8],h[9]);
s=u; t=l;
printf("S= %lX",s);
printf(" T= %lX",t);
printf(" PAT= %lX \n",pat);
} /* prelude */
- 25 -
void abcd()
{
a=0x2040801L;
b=0x804021L;
c=0xBFEF7FDFL;
d=0x7DFEFBFFL;
printf("A= %lX \n",a);
printf("B= %lX \n",b);
printf("C= %lX \n",c);
printf("D= %1X \n",d);
} /* abcd */
void inmain()
{
abcd();
printf("Press 1 to enter A,B,C,D,V,W,X0,Y0,M ");
printf("else <RET> for standard ABCD\n");
if ((getch())=='1') {
printf("Enter A (8 hex): \n"); scanf("%lX",&a);
printf("Enter B (8 hex): \n"); scanf("%lX",&b);
printf("~(8)=FFFFFFF7,~(4)=FFFFFFFB,~(6)=FFFFFFF9,~(3)=FFFFFFFC \n");
printf("~(1)=FFFFFFFE,~(2*)=7FFFFFFD,~(2)=FFFFFFFD \n");
printf("Enter C (8 hex): \n"); scanf("%lX",&c);
printf("Enter D (8 hex): \n"); scanf("%lX",&d);
printf("Enter V (8 hex): \n"); scanf("%lX",&v);
printf("Enter W (8 hex): \n"); scanf("%lX",&w);
printf("Enter X0 (8 hex): \n"); scanf("%lX",&x);
printf("Enter Y0 (8 hex): \n"); scanf("%lX",&y);
printf("Enter M (8 hex): \n"); scanf("%lX",&m);
} /* inmain */
void mainloop1(m)
unsigned long m;
{
unsigned long e,f,g;
printf("Results are in hexadecimal \n");
v=(v&BIT31)? (v<<1)|1L:v<<1; /* v=cyc(v); */
printf("V= %lX \n",v);
e=v^w; printf("E= %lX \n",e);
x=x^m; printf("X= %lX ",x);
y=y^m; printf(" Y= %lX \n",y);
f=e+y; printf("F= %lX ",f);
g=e+x; printf(" G= %lX \n",g);
f=f|a; printf("F= %lX ",f);
g=g|b; printf(" G= %lX \n",g);
f=f&c; printf("F= %lX ",f);
g=g&d; printf(" G= %lX \n",g);
x=mul1(x,f); printf("X= %lX ",x);
y=mul2a(y,g); printf(" Y= %lX \n",y);
} /* mainloop1 */
- 26 -
void mainloop2(m)
unsigned long m;
/* as mainloop1 without printf. Mul1, mul2a copied to save time */
{
unsigned long e,f,g,s;
int car;
v=(v&BIT31)? (v<<1)|1L:V<<1; /* V=CYC(V); */
e=v^w;
x=x^m; y=y^m;
f=e+y; g=e+x;
f=f|a; g=g|b;
f=f&c; g=g&d;
/* x=mul1(x,f); */
mul32(x,f);
s=u+l;
car=((u^l)&BIT31)? !(s&BIT31):(u&BIT31)!=0;
x=(car) ? S+1L:S;
/* y=mul2a(y,g); */
mul32(y,g);
g=u+u;
s=g+l;
car=((g^l)&BIT31)? !(s&BIT31):(g&BIT31)!=0;
y=(car)? s+2L:s;
} /* mainloop2 */
/* NOTE. Time measurement is not standard C, hence may not be portable. */
/* Guesstime + fracsec uses the 1 second clock of MS-DOS. */
/* Works with Turbo and Zorland compilers. */
signed long fracsec()
{
unsigned long i;
i=0; t5=time(NULL);
do i++; /* count while waiting for next second */
while (time(NULL)==t5);
return (i);
} /* fracsec */
float guesstime()
/* Uses fracsec and time (which counts whole seconds). */
/* Probably most portable, may be least accurate if interrupted. */
/* OK for Turbo and Zorland versions 1 and 2. */
{
unsigned long i,j,secs;
t4=t5;
i=fracsec(); secs=t5-t4-1; j=fracsec();
if (i>j) i=j;
return (secs+(j-i)/(float)j);
} /* guesstime */
- 27 -
main()
{
unsigned long i,t1,t2;
long ti;
int nn,ii,choice,disp,car;
float tf;
t5=0;
do {
choice=menu1();
printf("Note all results (except time) are in hexadecimal \n");
switch(choice) {
case 1:{
printf(" Enter X (8 hex): \n"); scanf("%lX",&x);
printf(" Enter Y (8 hex): \n"); scanf("%lX",&y);
sum=x+y;
printf("Sum= %lX",sum);
car=((x^y)&BIT31) ? !(sum&BIT31):(x&BIT31)!=0;
printf(" Carry= %X \n",car);
sum=x+x;
car=(x&BIT31)!=0;
printf("2*X= %lX",sum);
printf(" Carry= %X\n",car);
printf("Product= %lX\n",x*y);
mul32(x,y);
printf("mul32 upper= %lX",u);
printf(" mul32 lower= %lX \n",l);
printf("cyc= %lX\n",((x<<1)|((x&BIT31)>>31)));
printf("mul1= %lX\n",mul1(x,y));
printf("mul2= %lX\n",mul2(x,y));
printf("mul2a= %lX\n",mul2a(x,y));
byt(x,y);
printf("byt upper= %lX",u);
printf(" byt lower= %lX\n",l);
printf("pat= %X\n",pat);
}; break;
case 2:{
printf(" Enter J1 (8 hex): \n"); scanf("%lX",&x);
printf(" Enter K1 (8 hex): \n"); scanf("%lX",&y);
prelude(x,y,1);
}; break;
case 3:{
inmain();
mainloop1(m);
z=x^y; printf("Z= %lX\n",z);
}; break;
- 28 -
case 4:{
printf(" Enter J (8 hex): \n"); scanf("%lX",&x);
printf(" Enter K (8 hex): \n"); scanf("%lX",&y);
prelude(x,y,0);
x=x0; y=y0; v=v0; abcd();
do {
printf(" Enter M (8 hex): \n"); scanf("%lX",&m);
mainloop2(m);
printf("X= %lX",x); printf(" Y= %lX\n",y);
printf("Press 1 for coda else <RET> for another message \n");
} while ((getch())!='1');
mainloop2(s);
printf("X= %lX",x); printf(" Y= %lX\n",y);
mainloop2(t);
printf("X= %lX",x); printf(" Y= %lX\n",y);
z=x^y; printf("Z= %lX\n",z);
}; break;
case 5:{
printf(" Enter J (8 hex): \n"); scanf("%lX",&x);
printf(" Enter K (8 hex): \n"); scanf("%lX",&y);
prelude(x,y,0);
x=x0; y=y0; v=v0; abcd();
printf(" Enter M (8 hex): \n"); scanf("%lX",&m);
printf(" Enter number of repeated message blocks: \n");
scanf("%d",&nn);
printf(" Press 1 to display X,Y values ");
printf("else RET to measure time\n");
disp=getch();
if (disp=='1') {
for (ii=1; ii<=nn; ii++) {
mainloop2(m);
printf("X= %lX",x); printf(" Y= %lX\n",y);
}
printf(" Press a key to proceed \n"); disp=getch();
}
else {
i=fracsec();
for (ii=1; ii<=nn; ii++) {mainloop2(m);}
tf=guesstime();
printf("Seconds in mainloop (guesstime)= %6.2f\n",tf); i=i;
printf("Millisecs per message block= %6.2f\n",tf*1000.0/nn);
}
printf("X= %lX",x); printf(" Y= %lX\n",y);
mainloop2(s);
printf("X= %lX",x); printf(" Y= %lX\n",y);
mainloop2(t);
printf("X= %lX",x); printf(" Y= %lX\n",y);
z=x^y; printf("Z= %1X \n",z);
}; break;
}
} while (choice!=6);
} /* main */
- 29 -
23 Implementation in Basic
This version was originally developed on a BBC Model B micro, and also runs
with the M-TEC BBCBASIC(86) interpreter [3] on IBM compatibles. Both of
these interpreters provide 32 bit arithmetic and boolean functions.
The function ADDU executes unsigned addition and also leaves the value of
the carry bit in the variable CAR%. It is designed to avoid causing
overflow. There are many different ways of programming unsigned
addition, the choice being between using conditional statements or complicated
boolean expressions. The speed will depend upon the characteristics of
the compiler or interpreter. The method shown was the fastest found
using M-TEC Basic.
Multiplication is performed by the procedure MUL32 (which uses MUL16) to
produce a 64 bit unsigned product in U% and L%.
In the Prelude, the J values, K values and H values are stored in
individual variables although they could equally well be stored in arrays.
- 30 -
10 *KEY4SAVE"MAA7B05.BBC"|M
20 REM Message Authenticator Algorithm by D W Davies 1983
30 REM Version in 32 bit Basic for signed arithmetic by D O Clayden 1987
40 REM Copyright NPL 1987
50 REM Works correctly on BBC Model B
60 REM and in MTEC BBCBASIC(86) on IBM compatible PCs
70 :
80 DIM ABYT%(8)
90 VDU15
100 G4%=&40000000: G8%=&80000000: G3F%=&3FFFFFFF: REM GLOBAL CONSTANTS
110:
120 ON FNMENU1 GOTO140,320,360,400,530,680
130 :
140 PROCFETCH("X","Y",8)
150 SUM%=FNADDU(X%,Y%)
160 PRINT"SUM= ";~SUM%
170 PRINT"CARRY= ";CAR%
180 PROCMUL32(X%,Y%)
190 PRINT"MUL32 UPPER= ";~U%;" LOWER= ";~L%
200 PROD%=FNMUL1(X%,Y%)
210 PRINT"MUL1= ";~PROD%
220 PROD%=FNMUL2(X%,Y%)
230 PRINT"MUL2= ";~PROD%
240 PROD%=FNMUL2A(X%,Y%)
250 PRINT"MUL2A= ";~PROD%
260 PROCBYT(X%,Y%)
270 PRINT"BYT UPPER= ";~U%;" LOWER= ";~L%;;" PAT= ";~PAT%
280 PROD%=FNCYC(X%)
290 PRINT"CYC= ";~PROD%
300 GOTO120
310 :
320 PROCFETCH("J1","K1",8)
330 PROCPRELUDE(X%,Y%,1)
340 GOTO120
350 :
360 PROCINMAIN
370 PROCMAIN1(M%)
380 GOTO120
- 31 -
390 :
400 PROCFETCH("J","K",8)
410 PROCPRELUDE(X%,Y%,0)
420 X%=X0%: Y%=Y0%: V%=V0%
430 PROCABCD
440 INPUT"MESSAGE (8HEX)",T$:M%=EVAL("&"+T$)
450 PROCMAIN2(M%)
460 INPUT"Press 1 for Coda and exit else RET for more message",I%
470 IF I%=0 THEN 440
480 PROCMAIN2(S%)
490 PROCMAIN2(T%)
500 Z%=X%EORY%:PRINT"Z=";~Z%
510 GOTO120
520 :
530 PROCFETCH("J","K",8)
540 PROCPRELUDE(X%,Y%,0)
550 X%=X0%: Y%=Y0%: V%=V0%
560 PROCABCD
570 INPUT"MESSAGE (8HEX)",T$:M%=EVAL("&"+T$)
580 INPUT"Enter number of repeated message blocks",BLOCKS%
590 FOR NN%=1 TO BLOCKS%
600 PROCMAIN2(M%)
610 IF NN%MOD10=0 THEN INPUT"Press RET to continue":INPUTZ%
620 NEXT
630 PROCMAIN2(S%)
640 PROCMAIN2(T%)
650 Z%=X%EORY%:PRINT"Z=";~Z%
660 GOTO120
670 :
680 END
690 :
- 32 -
690 :
700 DEF FNADDU(X%,Y%)
710 LOCALS%,T%
720 S%=(X%ANDG3F%)+(Y%ANDG3F%)
730 T%=X%EORY%
740 IF T%ANDG4% THEN CAR%=S%ANDG4%:S%=S%EORG4% ELSE CAR%=X%ANDG4%
750 IF CAR% THEN S%=S%EORG8%
760 IF T%ANDG8% THEN CAR%=S%ANDG8%:S%=S%EORG8% ELSE CAR%=X%ANDG8%
770 IF CAR% THEN CAR%=1
780 =S%
790 :
800 DEF FNMUL16(X%,Y%)
810 LOCAL P1%,P2%
820 IF (X%ANDY%AND&8000)=0 THEN =X%*Y%
830 P1%=X%*(Y%AND&7FFF)
840 P2%=(X%AND&7FFF)*&8000
850 P1%=FNADDU(P1%,P2%)
860 =FNADDU(P1%,&40000000)
870 :
880 DEF PROCMUL32(X%,Y%)
890 LOCAL XU%,XL%,YU%,YL%,P1%,P2%,H8%,H10%,HF%,H7F%
900 H8%=&8000: H10%=&10000: HF%=&FFFF: H7F%=&7FFF0000
910 XU%=(X%ANDH7F%)DIVH10%
920 IF X%<0 THEN XU%=XU%+H8%
930 XL%=X%ANDHF%
940 YU%=(Y%ANDH7F%)DIVH10%
950 IF Y%<0 THEN YU%=YU%+H8%
960 YL%=Y%ANDHF%
970 L%=FNMUL16(XL%,YL%)
980 P1%=FNMUL16(XL%,YU%)
990 P2%=FNMUL16(XU%,YL%)
1000 P1%=FNADDU(P1%,P2%)
1010 U%=(P1%ANDH7F%)DIVH10%
1020 IF P1%<0 THEN U%=U%+H8%
1030 U%=U%+CAR%*H10%
1040 P1%=(P1%ANDHF%)*H8%
1050 P1%=FNADDU(P1%,P1%)
1060 L%=FNADDU(L%,P1%)
1070 U%=U%+CAR%
1080 P1%=FNMUL16(XU%,YU%)
1090 U%=FNADDU(U%,P1%)
1100 ENDPROC
1110:
1120 DEF FNMENU1
1130 LOCAL N%
1140 PRINT'"Message Authenticator Menu"
1150 PRINT"1 Test small functions (Tables 1,2)"
1160 PRINT"2 Test Prelude (Table 3)"
1170 PRINT"3 Test Main (Table 4)"
1180 PRINT"4 Test Prelude+Main+Coda (Table 5)"
1190 PRINT"5 Test repeated message blocks (Table 6)"
1200 PRINT"6 Quit"
1210 INPUT"Select by number",N%
1220 IF (N%<1)OR(N%>6) THEN 1140
1230 =N%
- 33 -
1240 :
1250 DEF PROCFETCH(A$,B$,N%)
1260 LOCAL T$
1270 PRINTA$;" (";N%;"HEX)";:INPUTT$:X%=EVAL("&"+T$)
1280 PRINTB$;" (";N%;"HEX)";:INPUTT$:Y%=EVAL("&"+T$)
1290 ENDPROC
1300 :
1310 DEF FNMUL1(X%,Y%)
1320 LOCAL S%
1330 PROCMUL32(X%,Y%)
1340 S%=FNADDU(U%,L%)
1350 =FNADDU(S%,CAR%)
1360 :
1370 DEF FNMUL2(X%,Y%)
1380 LOCAL D%,F%,S%
1390 PROCMUL32(X%,Y%)
1400 D%=FNADDU(U%,U%)
1410 F%=FNADDU(D%,CAR%+CAR%)
1420 S%=FNADDU(F%,L%)
1430 =FNADDU(S%,CAR%+CAR%)
1440 :
1450 DEF FNMUL2A(X%,Y%)
1460 LOCAL D%,S%
1470 PROCMUL32(X%,Y%)
1480 D%=FNADDU(U%,U%)
1490 S%=FNADDU(D%,L%)
1500 =FNADDU(S%,CAR%+CAR%)
1510 :
1520 DEF FNCYC(X%)
1530 =FNADDU(X%,X%)+CAR%
1540 :
1550 DEF PROCBYT(X%,Y%)
1560 LOCAL I%,P%
1570 FOR I%=3 TO 0 STEP-1
1580 ABYT%(I%)=X%AND&FF:ABYT%(I%+4)=Y%AND&FF
1590 IF X%>=0 THEN X%=X%DIV&100 ELSE X%=(X%AND&7FFFFFFF)DIV&100+&800000
1600 IF Y%>=0 THEN Y%=Y%DIV&100 ELSE Y%=(Y%AND&7FFFFFFF)DIV&100+&800000
1610 NEXT
1620 P%=0
1630 FOR I%=0 TO 7
1640 P%=P%*2
1650 IF ABYT%(I%)=0 THEN P%=P%+1:ABYT%(I%)=P% ELSE
IF ABYT%(I%)=&FF THEN P%=P%+1:ABYT%(I%)=&FF-P%
1660 NEXT
1670 PAT%=P%
1680 X%=0:Y%=0
1690 FOR I%=0 TO 3
1700 X%=X%*&80:X%=FNADDU(X%,X%)
1710 Y%=Y%*&80
1720 Y%=FNADDU(Y%,Y%)
1730 X%=X%+ABYT%(I%)
1740 Y%=Y%+ABYT%(I%+4)
1750 NEXT
1760 U%=X%:L%=Y%
1770 ENDPROC
- 34 -
1780 :
1790 DEF PROCPRELUDE(X%,Y%,TEST%)
1800 LOCAL P%,Q%,J1%,J12%,J22%,J14%,J24%,J16%,J26%,J18%,J28%
1810 LOCAL K1%,K12%,K22%,K14%,K24%,K15%,K25%,K17%,K27%,K19%,K29%
1820 LOCAL H0%,H4%,H5%,H6%,H7%,H8%,H9%
1830 PROCBYT(X%,Y%)
1840 J1%=U%: K1%=L%: P%=PAT%
1850 PRINT"P=";~P%
1860 IF TEST% THEN J1%=X%:K1%=Y%:INPUT"P",P%
1870 Q%=(1+P%)*(1+P%)
1880 J12%=FNMUL1(J1%,J1%)
1890 J22%=FNMUL2(J1%,J1%)
1900 J14%=FNMUL1(J12%,J12%)
1910 J24%=FNMUL2(J22%,J22%)
1920 J16%=FNMUL1(J12%,J14%)
1930 J26%=FNMUL2(J22%,J24%)
1940 J18%=FNMUL1(J12%,J16%)
1950 J28%=FNMUL2(J22%,J26%)
1960 H4%=J14%EORJ24%
1970 H6%=J16%EORJ26%
1980 H8%=J18%EORJ28%
1990 PRINT"H4=";~H4%
2000 PRINT"H6=";~H6%
2010 PRINT"H8=";~H8%
2020 K12%=FNMUL1(K1%,K1%)
2030 K22%=FNMUL2(K1%,K1%)
2040 K14%=FNMUL1(K12%,K12%)
2050 K24%=FNMUL2(K22%,K22%)
2060 K15%=FNMUL1(K1%,K14%)
2070 K25%=FNMUL2(K1%,K24%)
2080 K17%=FNMUL1(K12%,K15%)
2090 K27%=FNMUL2(K22%,K25%)
2100 K19%=FNMUL1(K12%,K17%)
2110 K29%=FNMUL2(K22%,K27%)
2120 H0%=K15%EORK25%
2130 H5%=FNMUL2(H0%,Q%)
2140 H7%=K17%EORK27%
2150 H9%=K19%EORK29%
2160 PRINT"H0=";~H0%
2170 PRINT"H5=";~H5%
2180 PRINT"H7=";~H7%
2190 PRINT"H9=";~H9%
2200 PROCBYT(H4%,H5%)
2210 X0%=U%:Y0%=L%
2220 PRINT"X0=";~X0%;" Y0=";~Y0%'"PAT=";~PAT%
2230 PROCBYT(H6%,H7%)
2240 V0%=U%: W%=L%
2250 PRINT"V0=";~V0%;" W=";~W%'"PAT=";~PAT%
2260 PROCBYT(H8%,H9%)
2270 S%=U%: T%=L%
2280 PRINT"S=";~S%;" T=";~T%'"PAT=";~PAT%
2290 PRINT"END OF PRELUDE"
2300 ENDPROC
- 35 -
2320 DEF PROCINMAIN
2330 LOCAL T$
2340 INPUT"A (8HEX)",T$:A%=EVAL("&"+T$)
2350 INPUT"B (8HEX)",T$:B%=EVAL("&"+T$)
2360 INPUT"C (8HEX)",T$:C%=EVAL("&"+T$)
2370 INPUT"D (8HEX)",T$:D%=EVAL("&"+T$)
2380 INPUT"V (8HEX)",T$:V%=EVAL("&"+T$)
2390 INPUT"W (8HEX)",T$:W%=EVAL("&"+T$)
2400 INPUT"X (8HEX)",T$:X%=EVAL("&"+T$)
2410 INPUT"Y (8HEX)",T$:Y%=EVAL("&"+T$)
2420 INPUT"M (8HEX)",T$:M%=EVAL("&"+T$)
2430 ENDPROC
2440 :
2450 DEF PROCABCD
2460 A%=&02040801
2470 B%=&00804021
2480 C%=&BFEF7FDF
2490 D%=&7DFEFBFF
2500 ENDPROC
2510 :
2520 DEF PROCMAIN1(M%)
2530 LOCAL E%,F%,G%,T0
2540 T0=TIME
2550 V%=FNCYC(V%):PRINT"V=";~V%
2560 E%=V%EORW%:PRINT"E=";~E%
2570 X%=X%EORM%:PRINT"X=";~X%;
2580 Y%=Y%EORM%:PRINT" Y=";~Y%
2590 F%=FNADDU(E%,Y%):PRINT"F=";~F%;
2600 G%=FNADDU(E%,X%):PRINT" G=";~G%
2610 F%=F%ORA%:PRINT"F=";~F%;
2620 G%=G%ORB%:PRINT" G=";~G%
2630 F%=F%ANDC%:PRINT"F=";~F%;
2640 G%=G%ANDD%:PRINT" G=";~G%
2650 X%=FNMUL1(X%,F%)
2660 Y%=FNMUL2A(Y%,G%)
2670 PRINT"Seconds inside Main= ";(TIME-T0)/100
2680 PRINT"X=";~X%;" Y=";~Y%
2690 PRINT"X EOR Y=";~X%EORY%
2700 ENDPROC
2710 :
2720 DEF PROCMAIN2(M%)
2730 LOCAL E%,F%,G%,T0
2740 T0=TIME
2750 V%=FNCYC(V%)
2760 E%=V%EORW%
2770 X%=X%EORM%
2780 Y%=Y%EORM%
2790 F%=FNADDU(E%,Y%)
2800 G%=FNADDU(E%,X%)
2810 F%=F%ORA%
2820 G%=G%ORB%
2830 F%=F%ANDC%
2840 G%=G%ANDD%
2850 X%=FNMUL1(X%,F%)
2860 Y%=FNMUL2A(Y%,G%)
2870 PRINT"Seconds inside Main= ";(TIME-T0)/100
2880 PRINT"X=";~X%;" Y=";~Y%
2890 ENDPROC
- 36 -
24 References
[1] A Message Authenticator Algorithm Suitable for a Main Frame
Computer by D.W. Davies and D.O. Clayden. NPL Report DITC 17/83, February
1983.
[2] ISO 8731-2 Banking - Approved algorithms for message
authentication - Part 2: Message authenticator algorithm.
[3] BBCBASIC(86). An interpreter for BBC Basic which runs on
IBM compatibles under MS-DOS. M-TEC Computer Services (UK), Ollands
Road, Reepham, Norfolk NR10 4EL, UK.
Notes:
This document is an update for the 1983 original: 'A Message Authenticator
Algorithm Suitable for a Main Frame Computer' by D.W. Davies and D.O. Clayden,
NPL Report DITC 17/83, February 1983.
NPL and the authors have kindly given permission for the document to be
released into the Public Domain.
However, Donald Davies wishes to dissociate himself from the decision to
process the message in 1024 byte blocks. He believes this causes more
problems than it solves.
David Claydon kindly volunteered the programs from his archive.
These can be found in file
clayden.zip.
The file maa.c is a 'C' version that compiles under
Turbo C++ version 1.01. It was derived from the program in the
document.
There are some slight format differences between this document and the
original. These were felt necessary to improve readability of the
original. The first page of this document is a composite of the cover of
the original and its page 3.
There seems to have been an error in the original text, relating to the
variable H0 used in the prelude:
On page 9, in both references it was called: H'
On page 15, again it was called: H'
On page 24, the print string was: "Hd %1X \n"
On page 34, lines 1820, 2120, 2130 and 2160 it was called: HD%
On page 34, line 2160 the print string was: "HD="
This has been corrected in the document. However, in the files
received from David Clayden this error persists and has not been
corrected.
Also, there is an 'i = i;' statement at the end of the 'C' version.
This seems to be redundant. (end of 13th line up from the bottom of page
28)
Note: in the Basic version, '~' is used in a print statement to produce
hexadecimal output.
Attacks:
Don Coppersmith [no reference available] and Bart Preneel have made some
progress. See: twomacs.pdf.
Reproduction Details:
The document was scanned and OCR'ed. However, the original was typed
on a machine that did not distinguish between 'O' and '0' as well as '1' and
'l'. So, despite thorough checking, there may be problems.
The WP used was Word running under Windows 98. To produce postscript,
the Apple Laserwriter driver was used. Finally Adobe Distiller was used
to produce the .PDF version.
Although the original was done on A4 paper (8.27" by 11.69") there should
be enough space at the bottom for it to be printed on the US Letter size paper
(8.5" by 11").
Comments welcome:
Keith
Back to home page
MAA,MDC,hash,message authenticator,message digest,
czczcz,cryptographic hash,ISO 8731-2,Donald Davies,
David Clayden

