Abstract. A fast software encryption algorithm is described. The computation cost is about 20 simple machine code instructions per word, although a key dependent table has to be constructed for each new key. Table construction time is some hundreds of word encryption times. It is a word based algorithm with a running key.
The name for the system is Word Auto Key Encryption having the acronym WAKE.
We attempt to design an encryption system
for medium speed encryption of blocks, and of high security. It is intended to
be fast on most modern computers, and relies on repeated table use and having
a large state space. It assumes the data cache can hold a table of 256 words,
so that random access to larger blocks is avoided. The speed is partly
attained by putting requirements on the algorithm usage. The description
assumes words of 32 bits and four bytes to a word.
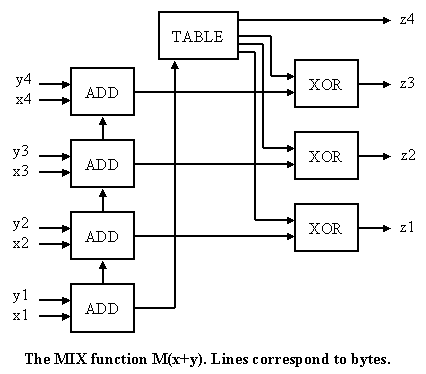
The nonlinear transforms are done by using
a table and alternating addition and XOR provides a little extra non
linearity. It takes the algorithm four stages for the word data to diffuse.
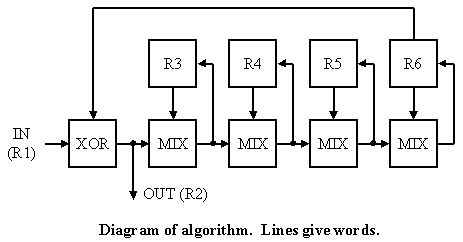
The full coding is performed by generating a table from a table key. Then the start key is used to initialise the registers R3-R6, and the program below is used to code each word, with those registers holding status information and acting as a running key or autokey. The content of the registers R3-R6 is saved as the end key, allowing disjoint sequences to be treated as one. A C program for the algorithm is given in the appendix. Let the vector being transformed be V[n].
For each n do
R1 = V[n]
R2 = R1 XOR R6
V[n] = R2
R3 = M(R3,R2) where M(X,Y)=(X+Y)>>8 XOR t[(X+Y) & 255]
R4 = M(R4,R3) and the table t has random bits apart from
R5 = M(R5,R4) the top byte whose value is different in
R6 = M(R6,R5) each location. The shift is logical.
A cyclic shift needs a different table.


Most modern computers will easily hold the
table in their cache, and we scan and replace the data words sequentially so
that only essential non cache references are made. There are about 12 simple
register operations per word cyphered.
Decoding is done by repeating the process,
with R2 in R3=M(R3,R2) replaced by R1. The initial values of R3-R6 must be the
same. The R variables should be kept in registers for best performance.
The main problem remaining is how to construct the table, and whether to give it special properties. The following program constructs the table from a table key and satisfies the obvious simple tests.
Copy K into first four words of t
Generate the other entries by
for n=4 to 255
x=T[n-1]+T[n-4]
T[n]= x>>3 XOR tt[x&7] where tt is a table of 8 words
having a permutation in the top
3 bits similarly to t.
Now add 23 elements from 89 onwards to element 0 onwards.
This makes even the first few words depend on all the key bits.
Generate a crude permutation in the top byte while further
mixing the lower bits.
Permute the table randomly using some bits of it to
control the permutation.
This needs three sweeps to generate the table. This heuristic table generation may have to be improved if further work shows more table properties are required or it is inadequate. A program in C is given in the appendix.
The basic operation will permute the bottom byte and place it in the top byte.
The original three top bytes are shifted down one byte and mixed using XOR
with three bytes from the table that generated the permutation.
This is reversible. From the result,
we can use the inverse permutation on the top byte to restore the
bottom byte, and XOR to recover the original word. The argument
is the sum of two registers and the result is put in one of these
registers. The addition is also reversible.
The consequence is that if one word is
changed, then the differences must propagate, although this will not show if
they are confined to R3-R6, an unlikely circumstance. To stop the propagation
will usually need changes to four consecutive words.
If any word is changed systematically and
the keys and other data remain fixed, one expects the cipher could be broken,
albeit using a large number of trials. It is assumed that the keys are
changed, sufficiently often to prevent this attack.
The table could be replaced by random
numbers but then, information leaks about repeated and null entries in the
table. This leakage may have a maximum limit of 1.5 bits per entry, but the
permutation reduces this statistical loss to a very small one indeed. However,
using a permutation for each of the four bytes might reduce this even further.
There are many ways in which WAKE can be used effectively. The
preferred way and the most straight forward is to extend the data
by 2 or more words at the head and tail, and fill the new head
and tail with a nonce or fresh random data, the same at both
ends. The decoder checks that tail words and the head words are
the same. Instead of equality we can use a known keyed relation,
but this is overkill for most simple uses. This protocol prevents
most attacks and gives tamper detection directly rather than as a
hoped for side effect. This we call mode one.
A second mode is to change the start key
for each data block.
A third mode, where these changes are
difficult, and we need the data to occupy exactly the same space, is a double
scan method. Just encode the block using a start key. Using another start key
encode in the reverse direction. This ensures that single bit changes are
likely to change about one half of all the generated bits. There is a slight
tail weakness, which can be cured by coding the last four words backwards
before doing the above.
The third mode can use a keyed hash
function of the same general type, having the same start key and the same
table to produce a four word hash. This hash can be thoroughly mixed with the
first four words, so that these change for each message, and we proceed as
before. The suggested hash function and protocol is given in the appendix. The
hash is nearly five times as fast as the cypher function.
The table key should be changed for long
messages, and may even be derived from the start key. If it is changed about
every ten thousand words, the slowing is about two or three per cent.
The overhead of generating the table may
be too large for short messages. Mode three can be used for short messages
using the same table. However, unless the start key is changed or the messages
known to be unique, for example numbered, the low entropy attacks are
possible.
Error propagation may have to be prevented
in some situations, such as video transmission. This can be done by changing
the running key as frequently as required and generating the running keys
using the same algorithm in a suitable way.
It is trivial to generate a sequence of
random numbers for use as a one time pad or for other purposes. A keyed hash
can be made readily. However the end key allows decryption, so it should be
further encoded before using it as an authenticator.
If the table t is known, then with five consecutive plain cipher
text pairs, we can determine the current values of R3-R6. If the
table is not known, a repeated change at one place may break the
table. This is prevented if a fresh start key is used each time.
There are other methods using salt, nonces, or confounders.
If a single scan is used then a change in
the last word will not propagate or be transformed. The usages given above
will prevent this happening. Another way is to use V[n]=R6 and endure the
slightly longer decryption. However whether this is a problem depends on other
details of the system, such as tamper detection. A one time pad using XOR
suffers more severely from this defect.
This is a word based algorithm, so for
transmissions between different computers, the big-end, little-end convention
has to be settled.
As each single line of the program is
reversible, we can make a slightly stronger version which is slower, by coding
with V[n]=R6, and using a more complicated decoding routine, using a table
derived from t.
The program processes about three bytes per microsecond on a
Sparc, ELC @ 33Mhz computer. Table generation of the form
described, takes the same time as coding about 250 words.
How secure is this algorithm? A few tests
have been applied. The distribution seems random. The loop lengths made with a
two step version seem of the right length, and there seems no obvious attack.
The large key and state spaces prevent some forms of attack.
The security can be enhanced by increasing
the number of stages in the basic algorithm from the four given, but at a
reduction in speed, however it is hoped that four stages will suffice.
Instead of using one table we can use a
separate table for each stage, with no loss in speed. As the tables would now
take four times as long to generate and four times as much space, we note that
the tables can be overlapped. In this case, some of the permutations have to
be restricted.
Although the algorithm is simple, it does need access to
convenient shift orders for ultimate speed. A logical right shift
is perhaps the easiest, and a cyclic shift made almost as easy.
In this case a simply transformed table is needed, with the left
most permutation byte p[n] being replaced by p[n] XOR n. The two
methods are then compatible. If only an arithmetic right shift is
available, then a masking operation is needed to be compatible.
We can use the arithmetic right shift without a masking
operation, and obtain an equally good but different encypherment.
In this case, it is more difficult to reverse some steps, but it
makes no difference for the simple case.
On some machines, the shifts which are
multiples of 8 may be replaced by byte operations. In particular, using the
leftmost byte for table look up in a byte operation may eliminate the shift
and mask operation.
The cypher routine given in the appendix
can be used for all the protocols suggested.
We have given a simple fast encyphering algorithm, suitable for
large bulk data, and for short messages where one key is changed.
It is suitable for keyed hashes, used for verification.
Its defects remain unknown to us, and so
should be pointed out.
The author would like to thank his Cambridge colleagues for useful interaction and Eli Biham for his help in improving this paper.
In the program below cypher is a function which changes the data V to become cyphered. V is the first or last word depending on the sign of n which gives the length. k gives the four words of the start key. r is loaded by the routine with the end key. t gives the 256 word encoding table.
cypher(V,n,k,r,t) long V[],n,k[], r[], t[] ; {
long r1,r2,r3,r4,r5,r6,d,*e,m=0x00ffffff ;
r3=k[0] ; r4=k[1] ; r5=k[2] ; r6=k[3] ;
if (n<0) d= -1 ; else d=1 ;
e=V+n ;
while (V-e) {
r1 = *V ;
r2 = r1^r6 ;
*V = r2 ; // Change into r1 for decoding.
V+ = d ;
r3 = r3+r2 ;
r3 = (r3>>8&m)^t[r3&255] ;
r4 = r4+r3 ;
r4 = (r4>>8&m)^t[r4&255] ;
r5 = r5+r4 ;
r5 = (r5>>8&m)^t[r5&255] ;
r6 = r6+r5 ;
r6 = (r6>>8&m)^t[r6&255] ; }
r[0] =r3 ; r[1]=r4 ; r[2]=r5 ; r[3]=r6 ; }
Mode three cyphering is done by
cypher(V+n-1,-4,k1,r,t) ;
cypher(V,n,k1,r,t) ;
cypher(V+n-1,-n,k2,r,t) ;
The cypher routine can encypher disjoint segments as if they were contiguous, by using a generated end key as the next start key. Thus for example we can put the head and tail for mode one wherever we please without moving the entire data structure.
genkey(t,k) long t[], k[] ; {
long x, z, p ;
static long tt[10]= {
0x726a8f3b, // table
0xe69a3b5c,
0xd3c71fe5,
0xab3c73d2,
0x4d3a8eb3,
0x0396d6e8,
0x3d4c2f7a,
0x9ee27cf3, } ;
for (p=0 ; p<4 ; p++) t[p]=k[p] ; // copy k
for (p=4 ; p<256 ; p++) {
x=t[p-4]+t[p-1] ; // fill t
t[p]=x>>3 ^ tt[x&7] ; }
for (p=0 ; p<23 ;
p++) t[p]+=t[p+89] ; // mix first entries
x=t[33] ; z=t[59] | 0x01000001 ;
z=z&0xff7fffff ;
for (p=0 ; p<256 ; p++) { //change top byte to
x=(x&0xff7fffff)+z ; // a permutation etc
t[p]=t[p] & 0x00ffffff ^ x ; }
t[256]=t[0] ; x&=255 ;
for (p=0 ; p<256 ; p++) { // further change perm.
t[p]=t[x=(t[p^x]^x)&255] ; // and other digits
t[x]=t[p+1] ; } }
The routine hash4 uses the mix, table and key as for the cypher function. The end words are mixed at least twice, and there is overlap if the length is not a multiple of four. This should make the hash nonlinearly dependant on all the data.
hash4(V,n,k,r,t) long V[],n,k[], r[], t[] ; {
long m, r3,r4,r5,r6,*e, mask=0x00ffffff ;
r3=k[0] ;r4=k[1] ; r5=k[2] ; r6=k[3] ;
e=V+n-3 ;
for (m=0 ; m<4 ; m++) {
while (V<e) {
r3=(r3^r6)+ *V++ ;
r3=(r3>>8 &mask)^t[r3&255] ;
r4=(r4^r3)+ *V++ ;
r4=(r4>>8 &mask)^t[r4&255] ;
r5=(r5^r4)+ *V++ ;
r5=(r5>>8 &mask)^t[r5&255] ;
r6=(r6^r5)+ *V++ ;
r6=(r6>>8 &mask)^t[r6&255] ; }
V =e-1 ; }
r[0]=r3 ; r[1]=r4 ; r[2]=r5 ; r[3]=r6 ; }
An example protocol would be ;
hash4(V+4,n-4,k,r,t) ; // hash in r from n-4 words
cypher(V,4,r,rr,t) ; // rr is a dump of four words
cypher(V+3,-4,r,rr,t) ; // mixes first four words
cypher(V,n,k,r,t) ; // do basic cypher
with decode
decypher(V,n,k,r,t) ;
hash4(V+4,n-4,k,r,t) ;
decypher(V+3,-4,r,rr,t) ;
decypher(V,4,r,rr,t) ;
Note we do not now need to do the end four words backwards, because the hash has a dependency on those four words.
Back to home page
block,cipher,block cipher,crypto,cryptography,cipher design,
encryption,word auto key,word autokey,WAKE,Hereward,David Wheeler,
czczcz,DJ Wheeler,David J Wheeler